Vectores

La palabra Vector vienen del latín «vector» «vectoris» y significa «que conduce».

¿Qué es un Vector?

Vector: todo segmento de una recta dirigido en el espacio.

Pero veamos mucho mejor qué es un vector con su uso.

Un vector se usa para describir una cantidad física, como la velocidad o la fuerza, que tiene una magnitud y una dirección.

De esta manera, por ejemplo, podemos describir cuán grande es la velocidad y en qué dirección se mueve, en un momento dado.

En matemáticas, a menudo contamos con vectores sin sus propiedades especiales, pero aún así decimos que el vector tiene tamaño y dirección.

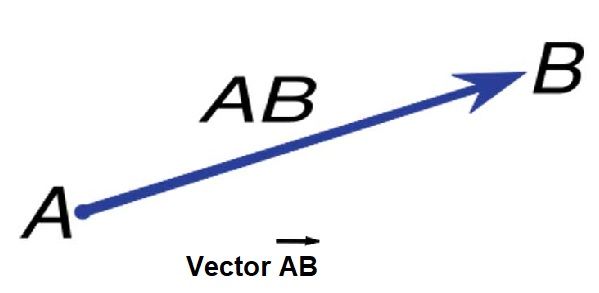
Si tienes un punto A y un punto B y dibujas una línea entre ellos, obtiene el segmento de línea AB.

Si esta línea tiene una dirección, es decir, el punto A «va hacia» el punto B, tenemos un vector.

Dibujamos y Escribimos el vector de A a B:

 

Los vectores, en física, nos sirven para representar una magnitud física como la velocidad o la fuerza. ¿Por qué?

Pues porque estas magnitudes tienen un punto de aplicación, un sentido y un valor, igual que los vectores, como veremos ahora.

Los vectores se representan por medio de flechas y cada vector posee una características.

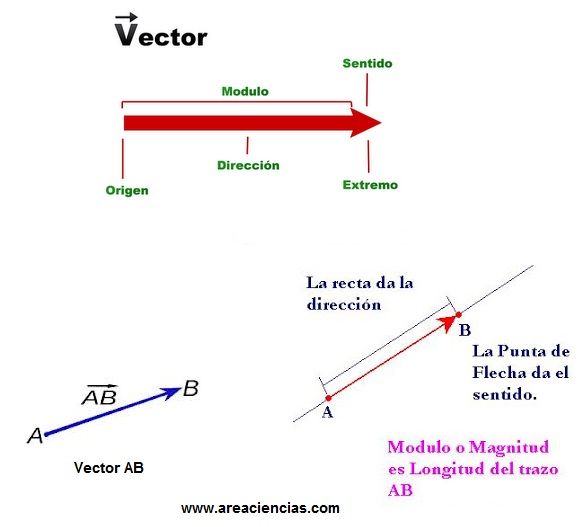
Características de un Vector

– Origen o Punto de Aplicación: es el punto exacto sobre el que actúa el vector.

– Módulo: es la longitud o tamaño del vector. Para saber el módulo de un vector es necesario conocer el punto inicial y final del vector (origen y extremo). Para calcular el módulo se mide desde el origen hasta el extremo.

– Dirección : viene dada por la orientación en el espacio de la recta que lo contiene. La recta que contiene el vector es su dirección, pero también es el ángulo que tiene el vector con respecto al eje de referencia. Si el eje de referencia es horizontal, el ángulo que forma el vector, con la horizontal, será la dirección.

– Sentido : se indica mediante una punta de flecha situada en el extremo del vector, indicando hacia que lado se dirige el vector.

A veces la combinación de la dirección y sentido se llama Orientación.

Generalmente los vectores tienen una letra en el origen y otra en el extremo, que dan nombre al vector.

Por ejemplo Va-b, vector ab, o simplemente AB (con una flecha encima de las letras para identificar que es un vector).

Proyecciones de un Vector

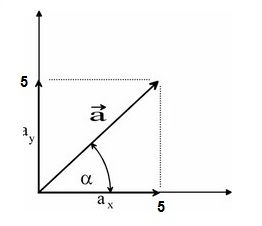
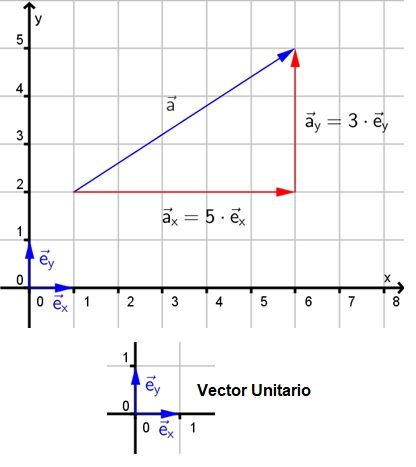
Un vector dentro de un plano cartesiano XY tiene dos proyecciones (dos componentes), una sobre el eje X y otra sobre el eje Y.

La descomposición de un vector, o lo que es lo mismo, los valores de estas dos componentes serán según Pitágoras:

ax será ax = cose ∝ * a

ay será ay = seno ∝ * a

También podríamos calcular el módulo de un vector, conocidos sus dos proyecciones (los catetos en el triángulo). El módulo del vector a sería la raíz cuadrada de ax2 + ay2 , ya que se cumple que a2 = ax2 + ay2 .

Fíjate que el vector a tiene un punto de inicio en el plano, en el ejemplo anterior x= 0 e y = 0, por lo tanto será el punto (0,0) y punto final, en el ejemplo anterior x = 5 e y = 5, por lo tanto el punto (5,5).

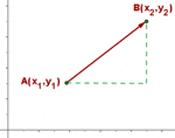
Según lo visto, un vector dentro de un plano cartesiano quedaría definido por su punto de origen y su punto final (coordenadas) dentro del plano.

En el ejemplo anterior sería a = (0,0), (5,5). Hay que poner la flecha arriba en la letra a, no la ponemos por que no nos lo permite el editor.

Pero si tomamos como referencia siempre el punto (0,0); solo con decir el punto final del vector ya quedaría definido.

En el caso anterior a = (5,5). Esto se suelo utilizar mucho por que casi siempre se toma como referencia el punto 0,0 como origen del vector.

Ojo podemos encontrarnos con vectores definidos por 3 puntos de coordenadas, por ejemplo a = (3, 4, 7), esto se debe a que esta en un plano tridimensional, es decir con coordenadas x, y, z.

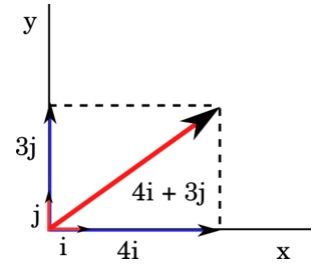
Otras veces nos encontraremos con vectores definidos de la siguiente forma a = 4i + 3j; esto simplemente lo que hace es decir que en el eje X la proyección del vector vale 4 y la proyección en el eje Y vale 3.

Se nombra al vector por sus proyecciones o componentes horizontal y vertical.

Esta forma de nombrar vectores se usa mucho en electricidad.

Veamos algunas operaciones con vectores

Suma de Vectores

Para realizar la suma de 2 vectores lo único que tenemos que hacer es sumar los componentes de los vectores, obteniéndose así el vector suma.

Esto se puede hacer de dos formas.

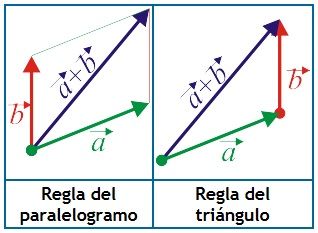
– Colocando un vector a continuación del otro, uniendo el final del primero con el origen del segundo. Este regla se llama regla del triángulo.

– Colocando los dos vectores en el mismo punto de inicio, la suma será la diagonal saliente del paralelogramo que nos queda. Esta regla se llama regla del paralelogramo.

Veamos un ejemplo:

Ahora veamos las propiedades de la suma de vectores, muy útil para simplificar operaciones. Hemos usado 3 vectores llamados u, v y w.

Si quieres ver ejemplos y ejercicios de suma de vectores te recomendamos este enlace: Suma de Vectores.

Resta de Vectores

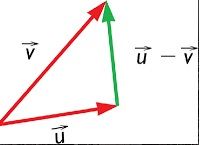
La resta de vectores gráficamente se realiza utilizando la regla de paralelogramo, pero en este caso el vector resta no será la diagonal saliente, sino la diagonal que une los dos extremos de los vectores, en dirección del vector más pequeño.

Veamos un ejemplo:

Si te fijas cuando restas un vector de otro lo que haces también es una suma, pero la suma del vector opuesto, por lo tanto las propiedades de la resta, son las mismas que la de la suma.

Producto de Vectores

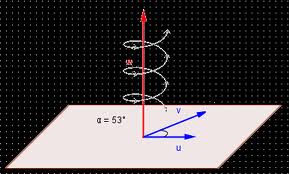
El producto vectorial de dos vectores es otro vector cuya dirección es perpendicular a los dos vectores y su sentido sería igual al avance de un sacacorchos al girar de uno a otro por el camino mas corto entre los dos (regla de la mano derecha).

El sacacorchos se entiende que gira hacia la izquierda siempre para sacarlos del corcho.

Su módulo es igual al producto del módulo de cada vector por el seno del ángulo que forman. Calcular solo el módulo se llama producto escalar de dos vectores..

Veamos un ejemplo:

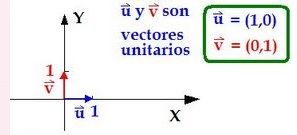
Vectores Unitarios

Un vector unitario se llama al vector que tiene como modulo la unidad (1).

Lógicamente un vector unitario tiene de módulo la unidad, pero también tiene una dirección y sentido, es esto precisamente lo que diferencia un vector unitario de otro.

Las coordenadas de un vector unitario también pueden ser cualquiera, ya que puede estar situado en el plano en cualquier punto.

Muchas veces se utiliza como unidad de medida el vector unitario.

Vectores Equipolentes

Se dice que dos o más vectores son equipolentes si tienen el mismo módulo, la misma dirección y el mismo sentido.

Como ves solo cambia la posición del vector dentro del plano, en lo demás son iguales.

Vectores con la Misma Dirección

Para saber si 2 vectores tienen la misma dirección, basta con mirar si sus coordenadas son proporcionales.

Veamos un ejemplo. vector a = ( 35, -21); vector b = (-10,6).

Miramos si son proporcionales dividiéndolas:

Coordenadas en X.  Las dividimos 35/-10; simplificando = 7/-2.

Coordenadas en Y . Las dividimos -21/6= -7/2

Como ves las coordenadas son proporcionales, quiere decir que esos dos vectores tienen la misma dirección.

Aquí te dejamos algunos ejercicios de vectores resueltos y explicados.

Si te ha la web «Vectores» gustado pulsa en Compartir. Gracias

© Se permite la total o parcial reproducción del contenido, siempre y cuando se reconozca y se enlace a este artículo como la fuente de información utilizada.