Indice de Contenidos
Desplazamiento Angular
Ya sabemos que el desplazamiento es la distancia desde la posición inicial hasta la posición final del movimiento de un cuerpo.
Además, el movimiento circular es cuando un cuerpo se mueve sobre un eje de giro y radio constante, por lo que su trayectoria será una circunferencia.
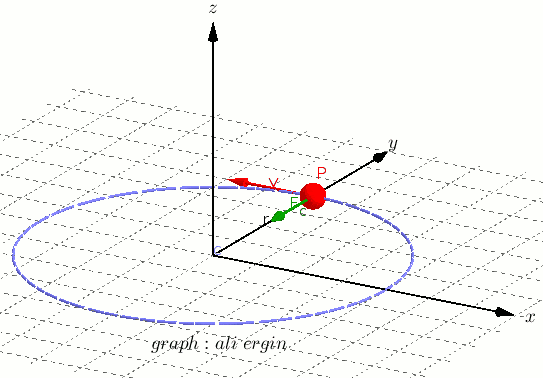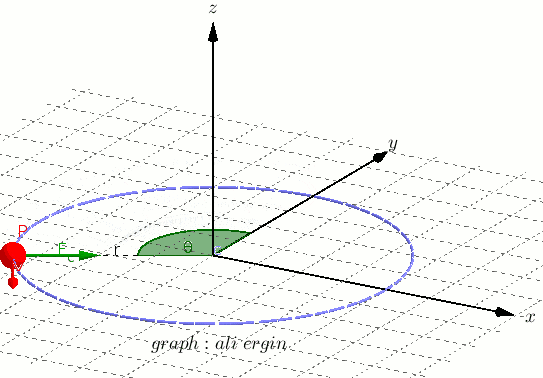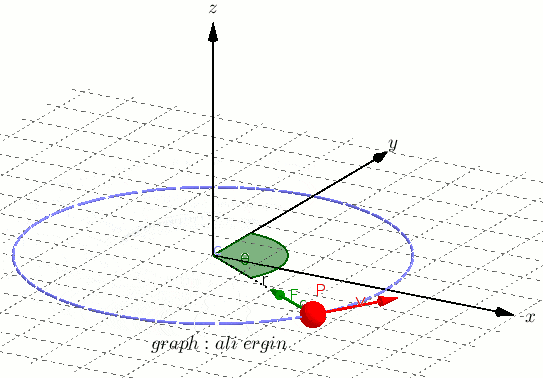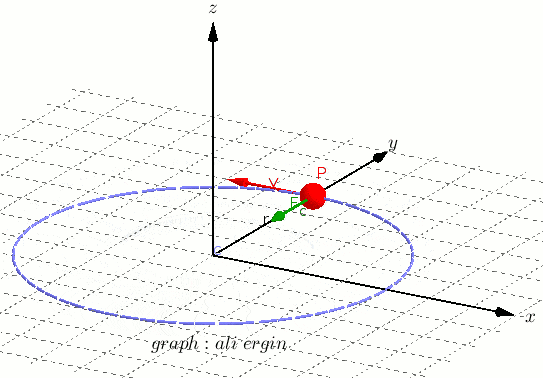
En la imagen se ve como el cuerpo se mueve con una velocidad constante, este movimiento será un movimiento circular uniforme.
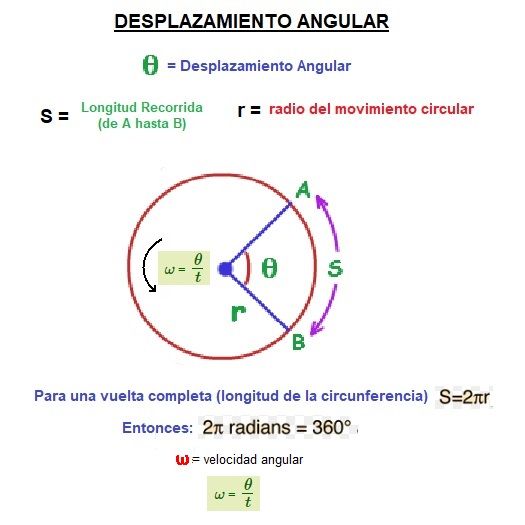
Puedes ver como el objeto al moverse por su trayectoria (circunferencia) describe un ángulo (θ ) que va aumentando hasta llegar a dar una vuelta completa.
Cuando da una vuelta completa, el ángulo ha recorrido 360º.
Cuando este ángulo que describe el movimiento circular se expresa en radianes se le llama «desplazamiento angular».
La longitud del desplazamiento de un objeto en movimiento circular es el desplazamiento angular (desplazamiento = distancia entre el punto inicial y el final), cuando esta longitud es el ángulo recorrido medido en radianes.
(θ f – θ i ) = θ; fórmula del desplazamiento angular.
Ya sabemos que 360º = 2π radianes.
El desplazamiento angular de 2π radianes equivale a una vuelta completa de la circunferencia del movimiento circular.
Mas adelante veremos como convertir grados a radianes y viceversa.
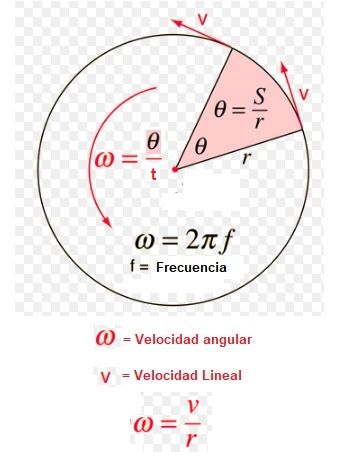
El desplazamiento angular se representa por la longitud del arco del camino curvado dividido entre el radio.
Esta longitud del arco se mide en el ángulo y, por lo tanto, el desplazamiento angular también se mide como un ángulo, en radianes.
Su unidad son radianes.
Otra fórmula para calcular el desplazamiento angular sería:
θ = s / r
θ = desplazamiento angular a través del cual se ha producido movimiento
s = distancia recorrida
r = radio del círculo
Hagamos un par de ejercicios para entenderlo mejor:
1) Un corredor recorre una pista circular que tiene un diámetro de 8,5 m.
Si recorre toda la pista en una distancia de 60 m, ¿Cuál es su desplazamiento angular?
Respuesta: El desplazamiento lineal del corredor, s = 60 m.
El diámetro de la trayectoria curva, diámetro = 8.5 m = 2radio, entonces radio = 4.25 m.
θ = s / r
θ = 60m /4.25 m
θ = 14.12 radianes
2) La panadería de un pequeño pueblo acaba de hacer un gran pastel de fresas para la apertura del festival de verano.
El pastel tiene un radio de 0.5 m.
Una mariquita aterriza sobre el pastel y camina alrededor del borde por una distancia de 80 cm.
¿Cuál es el desplazamiento angular de la mariquita?
Respuesta: La distancia recorrida por la mariquita, s = 80 cm = 0.08 m. El radio, r = 0.5 m.
θ = s / r
θ = 0.08m / 0.5 m
θ = 0.16 radianes
Velocidad Angular
Al igual que el movimiento lineal, el movimiento circular también tiene todas las cantidades equivalentes que tenemos en el movimiento lineal.
Ahora, veremos la velocidad angular.
La velocidad angular es la medida de lo rápido que un cuerpo está cambiando su ángulo y nos expresa la relación que existe entre el ángulo recorrido por nuestro objeto móvil y el tiempo empleado en recorrer dicho ángulo.
La velocidad angular se mide en radianes por segundo.
La velocidad angular está representada por le letra ω y, por lo tanto,
ω = θ / t; donde:
θ = desplazamiento angular (espacio recorrido expresado por el ángulo).
t = tiempo que tardó el objeto en recorrer el desplazamiento θ.
Relación entre velocidad lineal y velocidad angular
La Velocidad lineal y la Velocidad angular de cualquier cuerpo que se mueva en una trayectoria curva viene dada por:
v = ω x r; donde:
v = velocidad lineal,
ω = velocidad angular,
r = radio de la trayectoria curva.
Esta velocidad angular también se puede calcular en función del periodo y/o frecuencia de un movimiento circular.
Periodo Frecuencia y Velocidad Angular
En un movimiento circular uniforme constante, es decir que un objeto esté dando vueltas a la misma velocidad sin parar (velocidad angular fija), se llama periodo al tiempo que tarda en dar una vuelta completa el objeto.
Se representa por la letra T.
Hay muchos movimientos de este tipo, por ejemplo un alternador en corriente alterna para producir corriente eléctrica (generadores eléctricos).
En un periodo el objeto recorre 2π ángulos en radianes.
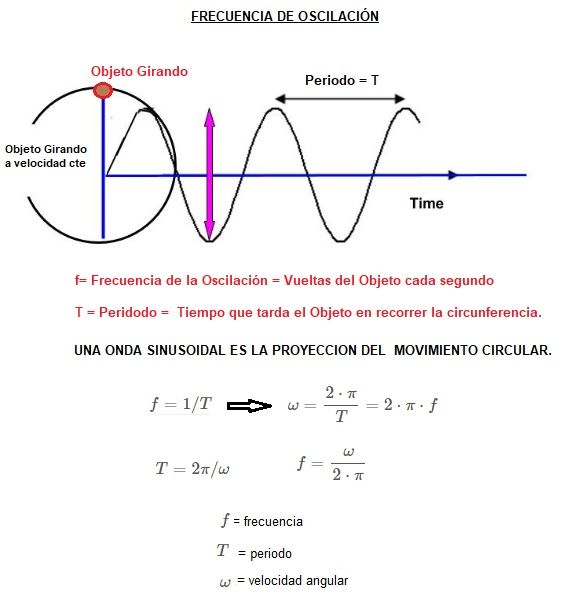
La frecuencia del movimiento son las vueltas que da el objeto, en ese movimiento, cada segundo.
También se llama frecuencia de la oscilación.
Además resulta que la frecuencia es la inversa del periodo:
f = 1 / T;
En estos casos podemos calcular la velocidad angular, sabiendo el periodo, y sabiendo que en un periodo (T) recorre una vuelta completa, 2π ángulos en radianes :
ω = espacio/tiempo = 2π /T;
Como f = 1 / T; ω también puede ser:
ω = 2π x f; donde f es la frecuencia de oscilación.
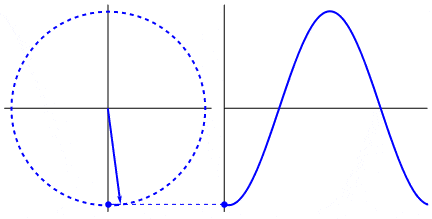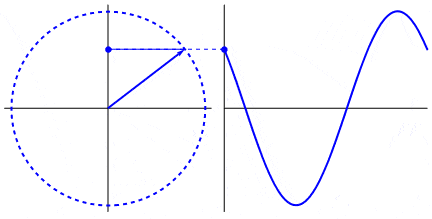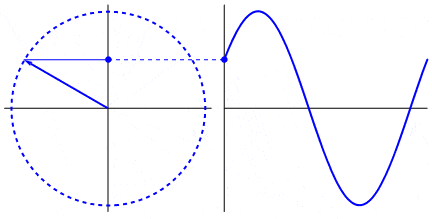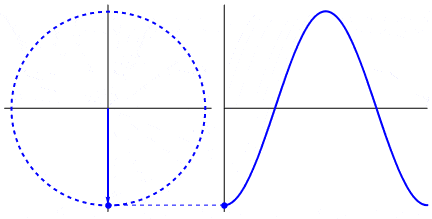
Estos movimiento se pueden representar por una onda senoidal o sinusoidal (seno).
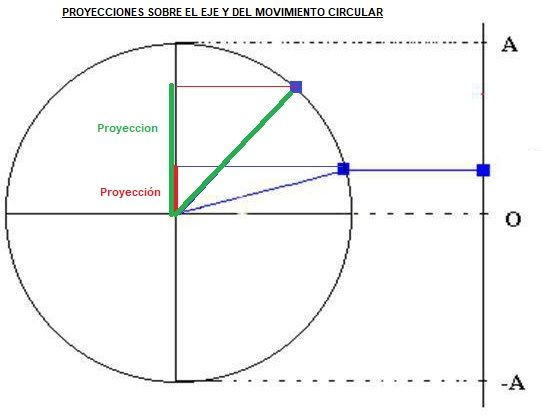
Fíjate que la onda senoidal representa los valores de la proyección del punto en movimiento sobre el eje Y (vertical).
Arriba del todo o abajo del todo la proyección es máxima y representa el radio del movimiento.
El movimiento sinusoidal es la proyección del movimiento circular.
Veamos algún ejercicio.
1) Una piedra gira en un movimiento circular con un radio de giro de 1m a razón de 6 vueltas por cada segundo.
¿Cuál será su velocidad angular?
Si la piedra hace cuatro rotaciones en un segundo, entonces su frecuencia se convierte en:
f = 6s-1
T = 1 / f = 1 / 6s
ω = 2π / T = (2π) / (1 / 6s) = 36 radianes/s
2) Considera la Tierra que gira sobre su eje una vez cada 24 horas.
Por lo tanto, la velocidad angular de la rotación de la Tierra es:
3)
Pasar de ángulos en Radianes a ángulos en Grados
Sabiendo que 360º son 2π radianes; π radianes = 180° media vuelta.
Si haces una regla de tres te saldrá que multiplicando los radianes por 180/π los conviertes en grados
Un ejemplo:
Una niña monta un tiovivo. Su asiento está a una distancia de 1 m del centro.
Si la chica se mueve a lo largo de un arco de 1.5 m.
¿Cuál es su desplazamiento angular?
¿Cuántos grados se desplazará la niña?
θ = s / r = 1,5 / 1 = 1,5 radianes; .
Los pasamos a grados; 180/π x 1,5 = 85,94º; Recuerda π = 3,1416.
Aquí tienes un enlace con Problemas de Velocidad Angular y Desplazamiento.
Si te ha gustado pulsa en Compartir. Gracias
© Se permite la total o parcial reproducción del contenido, siempre y cuando se reconozca y se enlace a este artículo como la fuente de información utilizada.

Sencillamente espectacular. Muchísimas gracias. Un comentario muy comedido: he observado que en España el símbolo para decimal, que en USA es «.», y en el resto de América es «,» están usando » ‘ «que aquí significa » unidades de millón» es que cambio la notación?, es usanza nueva?, o simple snobismo?. Gracias
Gracias por tu comentario. Ahora el símbolo es la coma «,» pero en la parte de arriba del número, cambió hace años. ¿Por qué? Pues ni idea jeje. Un saludo.
Muy buen contenido, práctico, ilustrativo y comprensible. Mis alumnos se convencieron de lo que es el desplazamiento angular y la velocidad angular; esto es aplicable en la vida diaria. Felicidades por hacer estas publicaciones didácticas y pedagógicas.
Otro tema de interés es:
– Movimiento en dos dimensiones
a) Tiro parabólico
b) Lanzamiento de un proyectil
Muchas gracias por el comentario. El tema de interés lo estudiaremos, gracias por la sugerencia. Un saludo.
Felicidades, explicado de una forma comprensible…para alguien de 65 años que está en esto para ayudar a su sobrino a entender el tema…!!!!
Felicidades a ti por ayudar a tu sobrino. Un saludo y gracias por el comentario.
Excelente presentación de la teoría angular, la recomiendo para todos aquellos padres cuyos hijos deben asistir a las facultades de ingeniería en universidades y que se encontraran con la aplicación de estos temas como parte de su carrera.
También para todos aquellos profesionales de las ramas de ingeniería que deseen refrescar estos conceptos útiles para aplicación practica.
Gracias por tu comentario que nos ayuda a seguir trabajando. Un saludo
Me encanta esta pag web, super recomendable 👌🏾👌🏾👌🏾