Las tres leyes de Kepler son fundamentales en astronomía y describen las principales propiedades del movimiento de los planetas alrededor del sol.
Estas leyes pueden extenderse a los cometas, así como a cualquier satélite del Sol o cualquier estructura del Universo.
Indice de Contenidos
Condiciones Para Cumplir las Leyes de Kepler
La condición es que la masa «m» del cuerpo estudiado sea insignificante en comparación con la del Sol, lo que se cumple para cualquier cuerpo del sistema solar, incluido el planeta Júpiter que es el más grande de los planetas del sistema solar.
Descubrimiento
Estas leyes fueron descubiertas por Johannes Kepler a partir de observaciones y medidas de la posición de los planetas realizadas por Tycho Brahé, medidas muy precisas para la época.
Las dos primeras leyes de Kepler se publicaron en 1609 y la tercera en 1618.
Copérnico había argumentado en 1543 que los planetas giraban alrededor del Sol , pero en órbitas circulares según el antiguo sistema de Ptolomeo.
Kepler introdujo las órbitas elípticas alrededor del Sol de los Planetas, como se indica en sus dos primeras leyes, ayudando a explicar la complejidad del movimiento aparente de los planetas en el cielo sin recurrir a modelos epicíclicos.
Poco después, Isaac Newton descubrió en 1687 la ley de atracción gravitacional (o gravitación), demostrando por cálculo las tres leyes de Kepler.
Primera Ley de Kepler
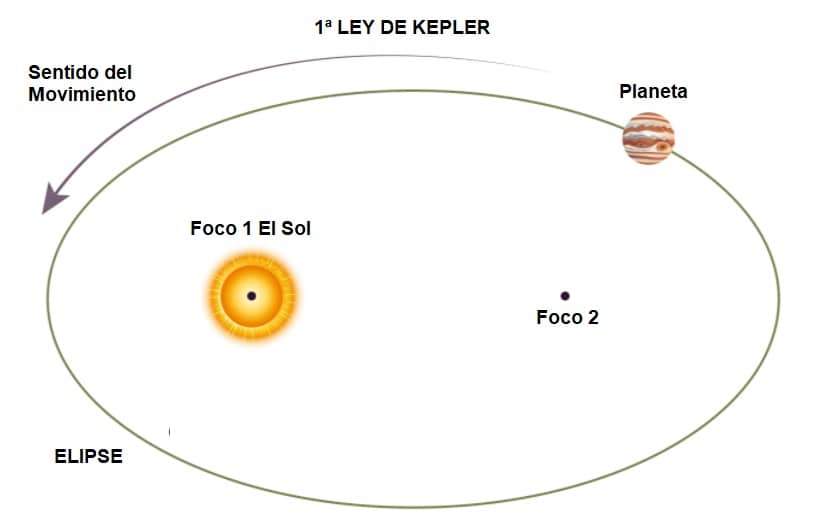
Primera ley de Kepler: Los planetas describen trayectorias elípticas de las cuales el Sol es un foco de la elipse que describe el planeta.
El Sol siempre ocupa uno de los dos focos de la trayectoria elíptica de los planetas que giran a su alrededor.
De esta primera ley, deducimos por cálculo que el sol ejerce una fuerza centrípeta sobre un planeta.
Nota: Fuerza Centrípeta es la fuerza que mantiene el movimiento circular del objeto (planeta).
Imagina que el Sol tiene atado a el mediante una cuerda al planeta y hace una fuerza que le hace girar.
Es como si tu tienes en una mano una cuerda y mueves girando un objeto en el extremo de la cuerda.
La fuerza la haces tu con la mano y es la responsable del movimiento giratorio del objeto en el extremo de la fuerza.
Segunda Ley de Kepler
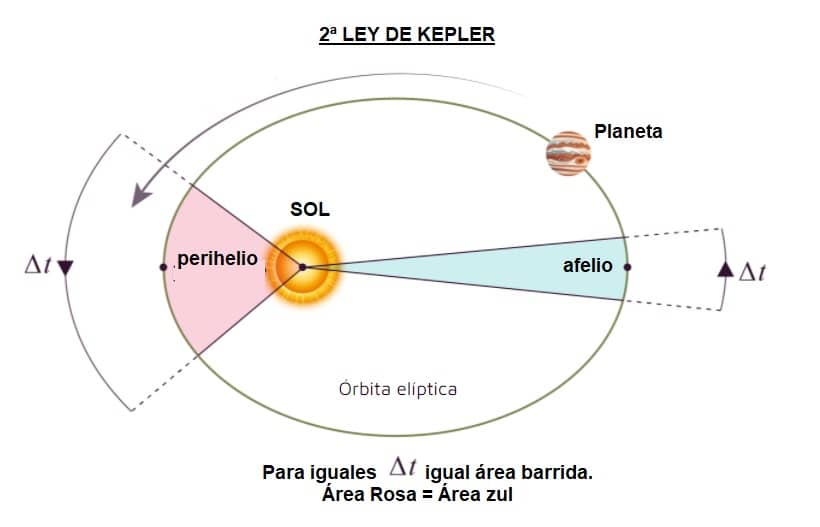
Segunda ley de Kepler: el rayo o eje del Sol hasta el planeta barre áreas iguales en su movimiento cuando los intervalos de tiempo son iguales.
Si «S» es el Sol y «M» cualquier posición de un planeta, el área escaneada por el segmento que une S con M entre dos posiciones C y D es igual al área barrida por este segmento entre otras dos posiciones, por ejemplo E y F, si la duración entre las posiciones C y D es igual a la duración entre las posiciones E y F .
De esto se deduce que la velocidad de un planeta aumenta cuando el planeta se acerca al sol.
El punto de la trayectoria más cercana al Sol se llama perihelio , y el punto más alejado del Sol se llama afelio.
En el diagrama anterior, se muestra el área escaneada para dos posiciones distintas, pero en el mismo lapso de tiempo Δ t.
La segunda ley de Kepler da como resultado la igualdad de las áreas rosadas y verdes.
De esta segunda ley deducimos que la fuerza que se ejerce sobre el planeta se dirige constantemente hacia el sol.
Tercera Ley de Kepler
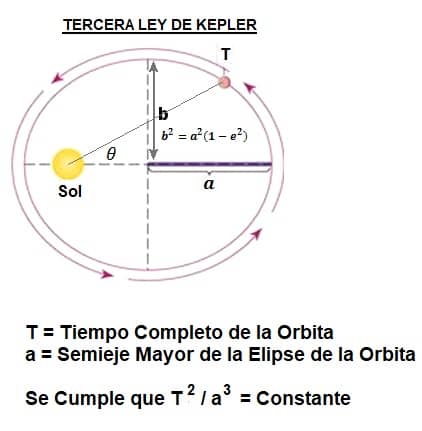
Tercera ley de Kepler: el cuadrado del período de revolución, tiempo que tarda en dar una vuelta completa a su órbita, es proporcional al cubo del semieje mayor de la órbita elíptica.
El cuadrado del período «T» de un objeto (tiempo entre dos pasajes sucesivos frente a una estrella distante) es directamente proporcional al cubo del semieje mayor «a» de la trayectoria elíptica del objeto:
«T» al cuadrado dividido entre «a» al cubo: (T ^ 2) / (a ^ 3) = k = una constante.
En el caso general donde la trayectoria es elíptica, la ecuación se escribe:
T²/a³ = (4pi²)/GM = k = constante
G = constante gravitacional universal y tiene el mismo valor en todo el universo.
G = 6,674 x 10-11 (10 elevado a menos 11)
De esta tercera ley, deducimos que existe un factor constante «k» entre la fuerza ejercida y la masa del planeta considerado, que es la constante gravitacional universal «G«.
Te recomendamos que veas para entenderlo mejor: Energía Potencial en el Espacio
Esta fórmula, junto con las de la elipse, permiten calcular los diferentes parámetros de una trayectoria elíptica a partir de muy poca información.
Si te ha gustado la página Las Leyes de Kepler pulsa en Compartir. Gracias
© Se permite la total o parcial reproducción del contenido, siempre y cuando se reconozca y se enlace a este artículo como la fuente de información utilizada.